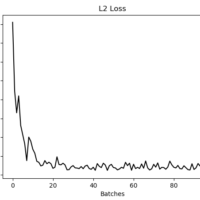
Linear Least Squares Regression is by far the most widely used regression method, and it is suitable for most cases when data behavior is linear. By definition, a line is defined by the following equation:

For all data points (xi, yi) we have to minimize the sum of the squared errors:

This is the equation we need to solve for all data points:

The solution for this equation is A (I’m not going to show how this solution is found, but you can see it in Linear Least Squares – Wikipedia, and some code in several programming languages as well), which is defined by:

Now, let’s see the implementation with TensorFlow:
import matplotlib.pyplot as plt
import tensorflow as tf
import numpy as np
sess = tf.Session()
x_vals = np.linspace(0, 10, num=100)
y_vals = x_vals + np.random.normal(loc=0, scale=1, size=100)
x_vals_column = np.transpose(np.matrix(x_vals))
ones_column = np.transpose(np.matrix(np.repeat(1, repeats=100)))
X = np.column_stack((x_vals_column, ones_column))
Y = np.transpose(np.matrix(y_vals))
X_tensor = tf.constant(X)
Y_tensor = tf.constant(Y)
tX_X = tf.matmul(tf.transpose(X_tensor), X_tensor)
tX_X_inv = tf.matrix_inverse(tX_X)
product = tf.matmul(tX_X_inv, tf.transpose(X_tensor))
A = tf.matmul(product, Y_tensor)
A_eval = sess.run(A)
m_slope = A_eval[0][0]
b_intercept = A_eval[1][0]
print('slope (m): ' + str(m_slope))
print('intercept (b): ' + str(b_intercept))
best_fit = []
for i in x_vals:
best_fit.append(m_slope * i + b_intercept)
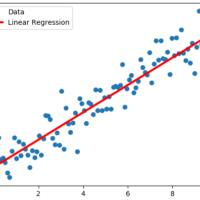
plt.plot(x_vals, y_vals, 'o', label='Data')
plt.plot(x_vals, best_fit, 'r-', label='Linear Regression', linewidth=3)
plt.legend(loc='upper left')
plt.show()slope (m): 1.0108287140073253
intercept (b): 0.14322921334345343

As you can see, the implementation is just executing basic matrix operations, the advantage of using TensorFlow in this case is that we can add this process to a more complex graph.