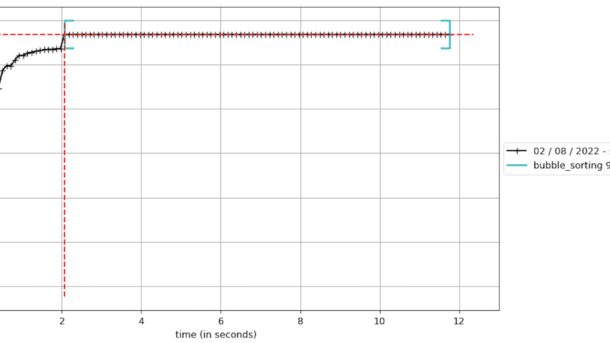
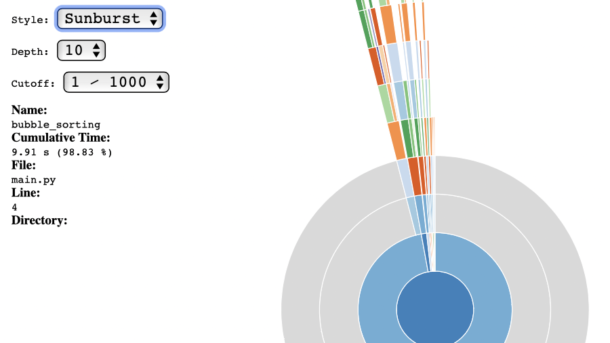
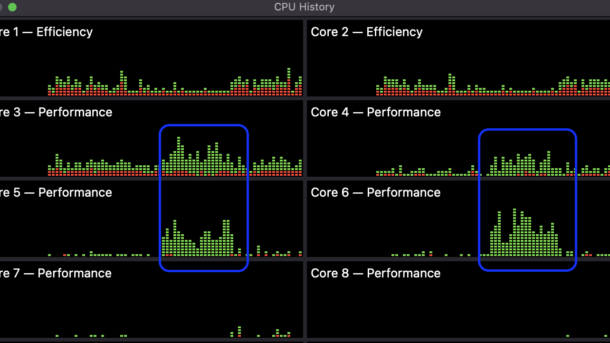
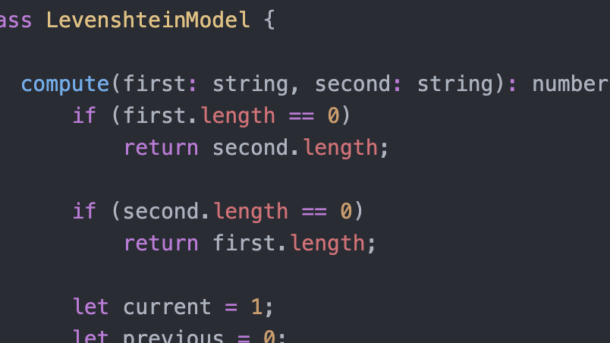
Introduction Hello, asyncio enthusiasts! If you’ve been following along, you’ll remember that we recently dived into the basics of Python’s asyncio library in our previous blog post. We explored the fundamentals like coroutines, tasks, and event loops, and even touched on some best practices and debugging techniques. But as promised,...
Continue reading...‘asyncio’ tutorial for the programmer in a hurry
Introduction In the evolving world of Python programming, understanding the asyncio library is becoming increasingly important. asyncio allows for asynchronous, concurrent, and parallel programming in a language that was traditionally synchronous and single-threaded. As Python applications grow in complexity and depend on I/O-bound tasks like web requests or database calls,...
Continue reading...Transformers: how do they work internally?
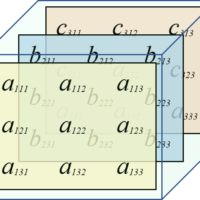
Table of Contents Introduction The Transformer is currently one of the most popular architectures for NLP. We can periodically hear news about new architectures and models based on transformers generating a lot of buzz and expectations in the community. Google Research and members from Google Brain initially proposed the Transformer...
Continue reading...Python Profiling – Memory Profiling (Part 3, Final)
Table of Contents memory_profiler PySpy DISassembling Final Recommendations memory_profiler Similar to line_profiler, memory_profiler provides detailed memory usage measurements, with the aim of efficiently reducing memory consumption and optimizing memory usage to improve application performance.. ⚠️ Before starting using this tool, it is important to mention the impact on the execution...
Continue reading...Python Profiling – cProfile and line_profiler Tools (Part 2)
Table of Contents cProfile SnakeViz, for cProfile insights Line-by-line Profiling About @profile decorator Other useful tools gprof2dot Pyinstrument Conclusion Appendix Install with pip or conda cProfile The Python standard library includes the profile tool by default; however, it additionally includes cProfile, which is an optimization of profile written in C....
Continue reading...Python Profiling – Time Profiling (Part 1)
Table of Contents Introduction Time Profiling Tools functools.wraps timeit module time / gtime Conclusion Introduction Many times, the code we write requires optimizations, and profiling helps us find the problematic sections of code, investing the least amount of work on fixing the issue, while aiming for the goal of gaining...
Continue reading...JavaScript Levenshtein Algorithm Implementation
One of the most known algorithms used by spell checkers and auto-complete fields is perhaps the Levenshtein algorithm, which basically minimizes the Levenshtein distance between the target word and the user input; or, in other words, the minimum number of missing characters and additions needed to transform a string into...
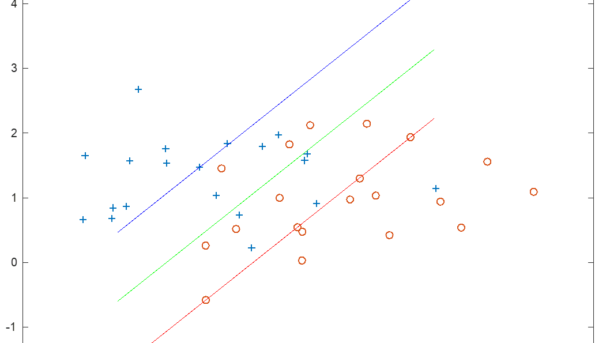
Continue reading...Support Vector Machines (SVM) for Classification
The purpose of this document is to present the linear classification algorithm SVM. The development of this concept has been based on previous ideas that have supported the development of SVM as an algorithm with good generalization capacity, based on an optimization criterion that minimizes complexity; with which we have...
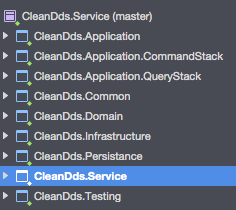
Continue reading...DDD Clean Architecture Template
(GitHub Repo: https://github.com/alulema/DDD-CleanArchitectureTemplate) These last 10 months I’ve been delighted working with ASP.NET Core, considering the improvements made by Microsoft to this framework, and the option to work on my Macbook as well However, an additional job to be done has been migrating the inherited skills and code snippets to its...
Continue reading...C# Sudoku Solver
(GitHub Repo: https://github.com/alulema/SudokuSolverNet) I was revisiting a couple of basic AI concepts: Depth First Search and Constraint Propagation, and I found a very good explanation by Professor Peter Norvig (Solving Every Sudoku Puzzle), I just want to add a couple of simple explanations for a better understanding of the concepts. Constraint...
Continue reading...