Descomposición Cholesky para Regresión Lineal

Ya han transcurrido varios años desde el inicio del auge del Deep Learning. He sido testigo de logros impresionantes como ChatGPT y Midjourney, sin embargo, aún me sorprende cómo métodos tradicionales como la descomposición Cholesky siguen siendo extremadamente útiles y eficientes. En particular, para tareas como la Regresión Lineal, este método destaca debido a su eficiencia y rapidez en el cálculo.

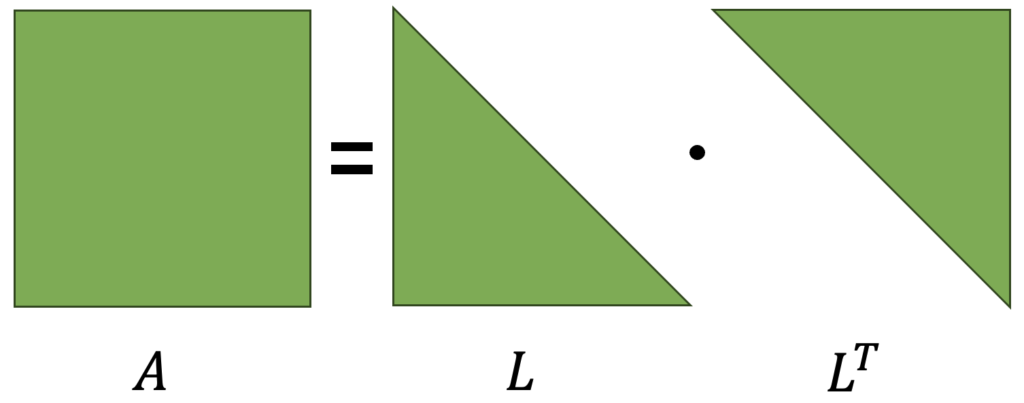
A pesar de que la Regresión Lineal de Mínimos Cuadrados es sencilla y precisa, puede volverse ineficiente cuando tratamos con matrices de gran tamaño. La descomposición Cholesky ofrece una alternativa para resolver estas matrices de manera eficaz. Esta técnica descompone una matriz en dos matrices triangulares: una inferior (lower) y una inferior transpuesta (L y L^T), con las cuales se obtiene la matriz original, tal como se ilustra en la figura que sigue.

\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ a_{21} & a_{22} & a_{23} & a_{24}\\ a_{31} & a_{32} & a_{33} & a_{34}\\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix}=\begin{bmatrix} l_{11} & 0 & 0 & 0\\ l_{21} & l_{22} & 0 & 0\\ l_{31} & l_{32} & l_{33} & 0\\ l_{41} & l_{42} & l_{43} & l_{44} \end{bmatrix}\cdot \begin{bmatrix} l_{11} & l_{21} & l_{31} & l_{41}\\ 0 & l_{22} & l_{32} & l_{42}\\ 0 & 0 & l_{33} & l_{43}\\ 0 & 0 & 0 & l_{44} \end{bmatrix}

El producto de la multiplicación de las dos matrices se muestra a continuación:

A=\begin{bmatrix} {l_{11}}^{2} & l_{21}l_{11} & l_{31}l_{11} & l_{41}l_{11}\\ l_{21}l_{11} & {l_{21}}^{2}+{l_{22}}^{2} & l_{31}l_{21}+l_{32}l_{22} & l_{41}l_{21}+l_{42}l_{22}\\ l_{31}l_{11} & l_{31}l_{21}+l_{32}l_{22} & {l_{31}}^{2}+{l_{32}}^{2}+{l_{33}}^{2} & l_{41}l_{31}+l_{42}l_{32}+l_{43}l_{33}\\ l_{41}l_{11} & l_{41}l_{21}+l_{42}l_{22} & l_{41}l_{31}+l_{42}l_{32}+l_{43}l_{33} & {l_{31}}^{2}+{l_{32}}^{2}+{l_{33}}^{2}+{l_{44}}^{2} \end{bmatrix}

A partir de este punto, cada elemento es una ecuación de las cuales se deduce lo siguiente:

Una característica (o limitación) de la descomposición Cholesky es que solo funciona en matrices positivas simétricas.

Finalmente, la regresión lineal mediante la descomposición Cholesky es análoga a los Mínimos Cuadrados Lineales, pero reducida a la resolución de un sistema de ecuaciones lineales.

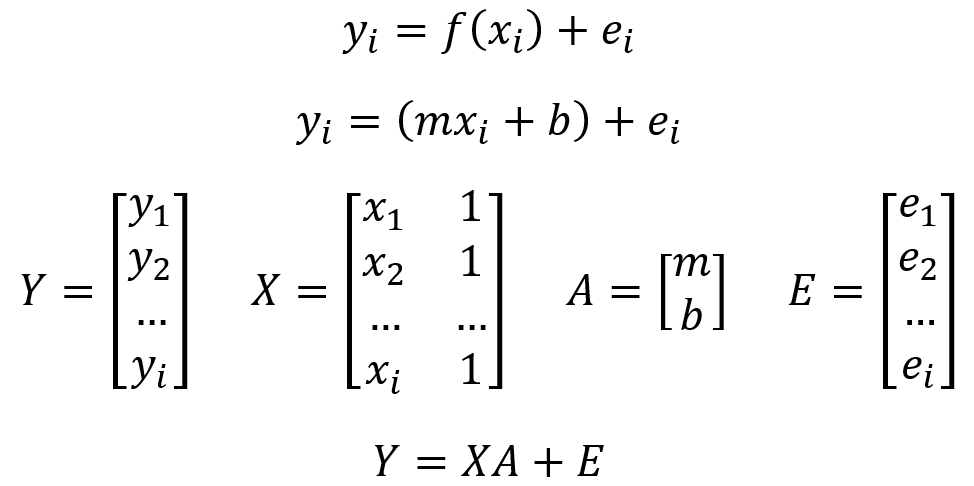
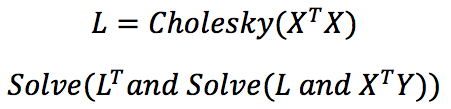
La descomposición Cholesky ya está implementada en TensorFlow, PyTorch o NumPy, sin embargo, en este link puedes revisar más detalles de Descomposición Cholesky.

Ahora, vamos a ver un ejemplo de su utilización:

import matplotlib.pyplot as plt
import tensorflow as tf
import numpy as np

# Generate data
x_vals = np.linspace(start=0, stop=10, num=100)
y_vals = x_vals + np.random.normal(loc=0, scale=1, size=100)

x_vals_column = np.transpose(np.matrix(x_vals))
ones_column = np.transpose(np.matrix(np.repeat(a=1, repeats=100)))
X = np.column_stack((x_vals_column, ones_column))
Y = np.transpose(np.matrix(y_vals))
X_tensor = tf.constant(X, dtype=tf.float64)
Y_tensor = tf.constant(Y, dtype=tf.float64)

# Perform computations
tX_X = tf.matmul(tf.transpose(X_tensor), X_tensor)
L = tf.linalg.cholesky(tX_X)
tX_Y = tf.matmul(tf.transpose(X_tensor), Y_tensor)
sol1 = tf.linalg.solve(L, tX_Y)
sol2 = tf.linalg.solve(tf.transpose(L), sol1)

# Extract coefficients
solution_eval = sol2.numpy()
m_slope = solution_eval[0][0]
b_intercept = solution_eval[1][0]

print('slope (m): ' + str(m_slope))
print('intercept (b): ' + str(b_intercept))

# Visualization
best_fit = []
for i in x_vals:
    best_fit.append(m_slope * i + b_intercept)

plt.plot(x_vals, y_vals, 'o', label='Data')
plt.plot(x_vals, best_fit, 'r-', label='Linear Regression', linewidth=3)
plt.legend(loc='upper left')
plt.show()

import matplotlib.pyplot as plt
import torch
import numpy as np

# Generate data
x_vals = np.linspace(start=0, stop=10, num=100)
y_vals = x_vals + np.random.normal(loc=0, scale=1, size=100)

x_vals_column = np.transpose(np.matrix(x_vals))
ones_column = np.transpose(np.matrix(np.repeat(a=1, repeats=100)))
X = np.column_stack((x_vals_column, ones_column))
Y = np.transpose(np.matrix(y_vals))
X_tensor = torch.tensor(X, dtype=torch.float64)
Y_tensor = torch.tensor(Y, dtype=torch.float64)

# Perform computations
tX_X = torch.mm(X_tensor.T, X_tensor)
L = torch.cholesky(tX_X)
tX_Y = torch.mm(X_tensor.T, Y_tensor)
sol = torch.cholesky_solve(tX_Y, L)

# Extract coefficients
m_slope = sol[0][0].item()
b_intercept = sol[1][0].item()

print('slope (m): ' + str(m_slope))
print('intercept (b): ' + str(b_intercept))

# Visualization
best_fit = []
for i in x_vals:
    best_fit.append(m_slope * i + b_intercept)

plt.plot(x_vals, y_vals, 'o', label='Data')
plt.plot(x_vals, best_fit, 'r-', label='Linear Regression', linewidth=3)
plt.legend(loc='upper left')
plt.show()

import matplotlib.pyplot as plt
import numpy as np

# Generate data
x_vals = np.linspace(start=0, stop=10, num=100)
y_vals = x_vals + np.random.normal(loc=0, scale=1, size=100)

x_vals_column = np.transpose(np.matrix(x_vals))
ones_column = np.transpose(np.matrix(np.repeat(a=1, repeats=100)))
X = np.column_stack((x_vals_column, ones_column))
Y = np.transpose(np.matrix(y_vals))

# Perform computations using Cholesky Decomposition
tX_X = np.dot(X.T, X)
L = np.linalg.cholesky(tX_X)
tX_Y = np.dot(X.T, Y)
sol = np.linalg.solve(L, tX_Y)
beta = np.linalg.solve(L.T, sol)

# Extract coefficients
m_slope = beta[0,0]
b_intercept = beta[1,0]

print('slope (m): ' + str(m_slope))
print('intercept (b): ' + str(b_intercept))

# Visualization
best_fit = []
for i in x_vals:
    best_fit.append(m_slope * i + b_intercept)

plt.plot(x_vals, y_vals, 'o', label='Data')
plt.plot(x_vals, best_fit, 'r-', label='Linear Regression', linewidth=3)
plt.legend(loc='upper left')
plt.show()

slope (m): 1.0830263227926582
intercept (b): -0.3348165868955632

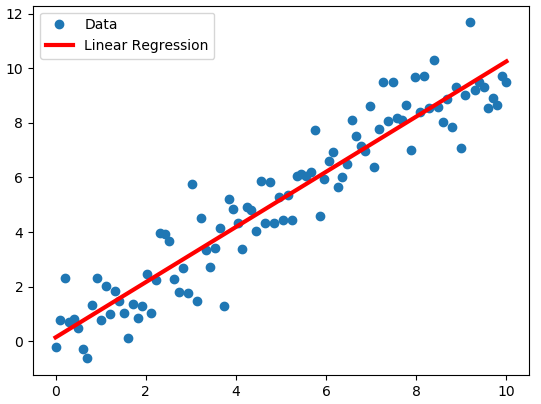
Como se puede observar, esta solución es muy similar a la Regresión Lineal de Mínimos Cuadrados, pero esta descomposición es a veces mucho más eficiente y numéricamente estable.

Etiquetas: pythonpytorchtensorflow